Vorwort
Diese Ausarbeitung betrachtet das Positionsbestimmungssystem GPS von einem mathematischen Blinkwinkel aus und gibt einen Überblick der rechnerischen Ortsbestimmung im dreidimensionalen Raum.
Einleitung
Bis zur Erfindung der Satelliten gestützten Navigation musste man sich umständlicher Hilfsmittel (z.B. geographische Besonderheiten, Gestirne, Kompass, etc…) bedienen, um sich in einer unbekannten Umgebung zu recht zu finden. Heut zu Tage gibt es 2 konkurrierende Satellitensysteme, das vom Verteidigungsministerium der ehemaligen Sowjetunion konzipierte Global Navigation Satellite System (GLONASS) und das amerikanische Äquivalent Global Positioning System (GPS). Obwohl beide Systeme als nahezu gleichwertig zu betrachten sind, hat sich das GPS durchgesetzt und wird im Folgenden genauer betrachtet.
Satelliten
Die GPS-Satelliten werden auch als Space- Segment bezeichnet. Sie befinden sich auf 6 Bahnen,

die in einer Entfernung von ca. 20230 km von der Erdoberfläche um die Erde verlaufen.
Das entspricht ca. der Hälfte der Entfernung eines geostationären Satelliten, so dass jeder Satellit die Erde pro Tag etwa 1 Mal umrundet. Die Bahnebenen sind bezüglich der Äquatorebene um ca. 55° geneigt (Inklination) und besitzen einen Rektaszensionsunterschied von 60°
(„Verschiebung entlang der Äquatorebene als Ring betrachtet“). Durch diese Anordnung werden mindestens 21 Satelliten benötigt, da zu jedem Zeitpunkt an jedem Ort 4 Satelliten gleichzeitig zu sehen sein müssen. Aus Redundanzgründen werden jedoch 28 zur Verfügung gestellt. Jeder Satellit ist mit eine
r Atomuhr ausgestattet, so dass die Uhren aller Satelliten synchron laufen. Da dies jedoch nicht immer vollständig gewährleistet werden kann, werden sie zusätzlich noch von Bodenstationen (dem sog. Controll- Segment) überwacht und gegebenenfalls von dort synchronisiert.
Ortsbestimmung
Die Ortsbestimmung im dreidimensionalen Raum ist der Hauptzweck von GPS. Dazu senden die Satelliten in regelmäßigen Zeitabständen Signale zur Erde, die dort von GPS-Empfängern empfangen und ausgewertet werden. Das Signal beinhaltet mehrere Datensegmente, von denen jedoch nur 2 für die Ortsbestimmung obligatorisch sind:
- Die Sendezeit des Signals
- Die Bahndaten bzw. die Position des Satelliten
Aus der Sendezeit des Signals lässt sich die Entfernung zwischen Sender und Satellit berechnen während die Positionen der Satelliten als Punkte in einem Koordinatensystem aufgefasst werden können.
Eindimensional synchron
In diesem Szenario gibt es einen Sender und einen Empfänger, wobei sich der Empfänger auf einer Geraden bezüglich des Senders bewegt. Sowohl Sender als auch Empfänger besitzen synchronisierte Uhren, so dass sich die Position des Empfängers mit der Formel
berechnen lässt.
Synchronisationsproblem (Eindimensional asynchron)
In der Realität ist es aus Kostengründen nicht möglich, jedes GPS-Gerät mit einer Atomuhr auszustatten. Dadurch scheint es zunächst unmöglich zu sein, die obige Gleichung zu lösen,
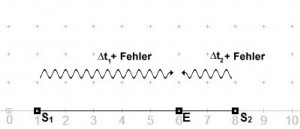
da die Laufzeit ?t nicht mehr korrekt bestimmt werden kann. Die Entfernung, die man erhält, wenn man die Laufzeit eines Signals bei asynchronen Uhren misst, wird als Pseudo-Range bezeichnet. Pseudo deshalb, weil die Uhr des Empfängers einen Fehler (Uhrenfehler) enthält (d.h. sie geht vor oder nach) und somit auch die Entfernung um einen Betrag, der eben diesem Uhrenfehler multipliziert mit der Ausbreitungsgeschwindigkeit des Signals entspricht, verschoben ist. Als Gleichung sähe das folgendermaßen aus: pr + L = v ? ?t , wobei pr dem berechneten Pseudo-Range und L der Verschiebung bzw. dem Entfernungsfehler entspricht Allerdings lässt sich die Position des Empfängers trotzdem ermitteln, wenn man noch einen weiteren Sender, der sich ebenfalls auf der Geraden des ersten Senders und des Empfängers befindet, einsetzt (siehe Abb. 2). Fasst man die Abbildung als eindimensionales Koordinatensystem auf, ergeben sich die folgenden Gleichungen:
Der Uhrenfehler Fehler kann also mit Hilfe des zweiten Satelliten „heraus gerechnet“ werden, so dass der GPS-Empfänger seine Uhr synchronisieren kann.
Zweidimensional asynchron
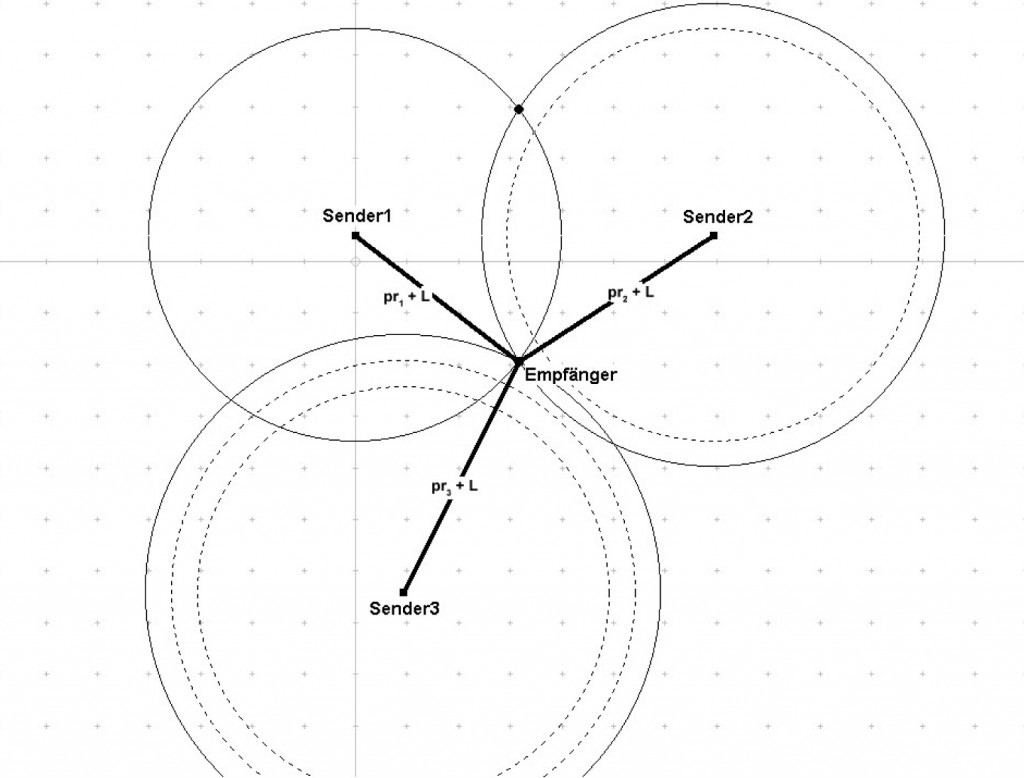
Der nächste Schritt der Ortsbestimmung ist die Lokalisierung des GPS-Empfängers in der Ebene. Diese enthält nun zwei Dimensionen, so dass insgesamt drei Sender zur genauen Positionsbestimmung benötigt werden. Da sich Funksignale mit gleicher Geschwindigkeit in alle Richtungen ausbreiten, formen sie in einem zweidimensionalen Koordinatensystem einen Kreis um den jeweiligen Sender. Dieser Kreis wird durch die allgemeine Kreisgleichung x² + y² = r² beschrieben. Daraus ergeben sich die folgenden Gleichungen für die „Signalkreise“ der einzelnen Sender:
Dieses nichtlineare Gleichungssystem enthält 3 Unbekannte X(Empfänger), Y(Empfänger) und L, so dass es mit Hilfe von Approximations- und Iterationsverfahren hinreichend genau gelöst werden kann. Abbildung 3 veranschaulicht dieses Verfahren:
Dreidimensional asynchron
Im dreidimensionalen Raum ergeben die Ausbreitungen der Signale nun Kugeln (statt Kreise), die der Gleichung x² + y² + z² = r² genügen. Zudem wird mit der weiteren Dimension auch ein zusätzlicher Satellit benötigt. Der mathematische Hintergrund ist analog zur zweidimensionalen Ortsbestimmung gegeben, so dass sich nun das folgende Gleichungssystem ergibt:
Relativistische Einflüsse
Bei der Betreibung der Satellitenuhren muss mit größter Umsicht agiert werden, da bereits eine Abweichung um 1 ?s einem Messfehler von ca. 300 m entspricht und somit das komplette System nutzlos wäre. Deshalb muss hier dem Einfluss der speziellen sowie der allgemeinen Relativitätstheorie Beachtung geschenkt werden. Der als „Zwillingsparadoxon“ bekannte Effekt der speziellen Relativitätstheorie besagt, dass sich die Zeit mit zunehmender Geschwindigkeit ausdehnt. Dies hätte zur Folge, dass ein Astronaut, der von einer Weltraumreise zurückkehrt, jünger ist, als sein Zwillingsbruder auf der Erde. Gleichzeitig muss die allgemeine Relativitätstheorie berücksichtigt werden, laut der eine Uhr umso langsamer geht, je größer das Gravitationspotenzial an ihrem Standort ist. Bezogen auf den Planeten Erde ist das Gravitationspotenzial eines Ortes proportional zu dem Verhältnis von der Masse der Erde zur Entfernung des Ortes vom Erdmittelpunkt. Demzufolge gehen die Uhren auf der Erde also langsamer als die in den Satelliten.
Zusammenfassung
Mit Hilfe von GPS ist nicht nur die genaue Ortsbestimmung eines Objektes im dreidimensionalen Raum möglich. Weitere Einsatzgebiete sind u.a. die Bestimmung von Geschwindigkeiten bewegter Objekte sowie die weltweite Synchronisation von Uhren. Allerdings deckt diese Ausarbeitung nur die prinzipielle, theoretische Funktionsweise von GPS ab. Im realen Einsatz müssen noch andere Variablen wie z.B. atmosphärische Störungen und Übertragungsfehler betrachtet werden. Der kurze Exkurs zu relativistischen Einflüssen macht die Komplexität dieser Thematik deutlich.
Literatur
- [HCUHA] Facharbeit aus der Mathematik: Global Positioning System
- http://www.hcu-hamburg.de/geomatik/geo/gps.htm Stand 11.11.2009
- [TUILM] GPS an der TU Ilmenau
- http://www.toralf-schumann.de/html/gps_prz.html Stand 11.11.2009
- [HSESS] GPS: Global Positioning System – Funktionsweise und mathematische Grundlagen
- http://www2.hs-esslingen.de/~abel/gps/Abel-GPS.htm Stand 11.11.2009
- [WIKIGPS] Wikipedia: Global Positioning System
- http:/de.wikipedia.org/wiki/Global_Positioning_System Stand 11.11.2009

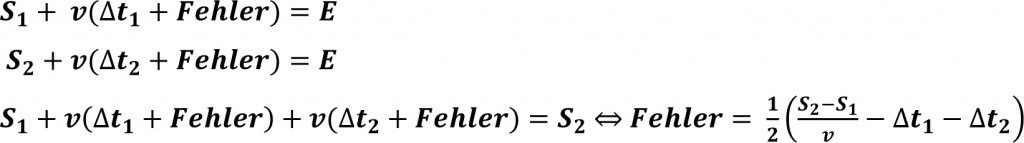


Will es für ein Physikreferat versthen: Liegt bei Eindimensional asynchron nicht ein Fehler vor? Wenn man die beiden Gleichungen gleichsetzt, steht nach umformen auf s_2 doch: s_1 + v (t_1 + Fehler) — v (t_2 + Fehler) = s_2
und nicht: s_1 + v (t_1 + Fehler) + v (t_2 + Fehler) = s_2